Low-noise Stills from Video

CSE 557 Final Project

Supasorn Suwajanakorn / Andre Baixo

Introduction

When taking photos under low-light environments such as indoor or at night, one of the two undesirable outcomes can happen: The photos can be blurry due to camera's or subjects' motion taken with long exposures or they can contain high level of noise because of short exposures and high sensor sensitivity. One approach that can overcome this problem is to capture a short video sequence or multiple high-noise photos and computationally combine them to produce a single low-noise photo.

Goals

Given a short video sequence (10-30 frames) taken from a hand-held camera, recover a low-noise still image. The algorithm should be robust to both camera's and scene motions and should be fast enough to provide a practical experience on mobile phones / cameras.

Related work

Algorithm

We studied some techniques used in related work and tried different combinations of the algorithms, but given a limited period of time, we were not able to experiment with full implementations of the reference papers. However, we came up with a reasonable compromise between algorithm's runtime, complexity, and quality. The following is a full description of our algorithm.

The first frame in the video sequence will be used as a reference frame for which we try to reduce the noise. On the reference frame, we detect features using SURF feature detector, then we track those feature points throughout the video sequence using Lucas-Kanade tracking method. These tracked features will provide sparse correspondences between each frame and the reference. We perspective-warp each frame to the reference by robustly solving for a 3 x 3 homography via RANSAC. Then we run polynomial expansion-based Farneback's optical flow algorithm between each frame and the reference which is fast and gives low interpolation error but has high endpoint and angular errors. The two latter errors however are not important in our task because we only care about image similarity. Suppose these aligned frames are $I^1, I^2, \dots, I^n$ and $I^0$ is the reference, we compute $D^i = G * (I^0 - I^i)$ where $G$ is a truncated Gaussian kernel of size 3 x 3 and $*$ is the convolution operator. Then we weight the contribution from each pixel in each frame based on color similarity. A noise-reduction version of $I^0$ is given by:

\wildetilde{I^0_{uv}} = \frac{1}{Z}\sum_{i=1}^nI^i_{uv} \exp(\frac{-\|D^i_{uv}\|^2}{2\sigma^2})
Z_{uv} = \sum_{i=1}^n \exp(\frac{-\|D^i_{uv}\|^2}{2\sigma^2})

$Z$ is the normalization factor and $D^i_{uv}$ is a vector that encodes RGB values for pixel $uv$. $\sigma$ controls the similarity weight.

This similarity-based weight can handle small scene motions, but for large motions, there can be cases where the average pixels are close to those of $I^0$ but represent different objects such as when the exact pose of a person in the reference frame, for example, appears in only a few frames and the average converges to a different value but close to the true value. In such case, it is sometimes more desirable to retain the noisy original pixels. One way to solve this problem is to apply a threshold to the color difference and retain original pixels when the sum is too large. Again, to make the algorithm more robust against noise, the sum of color differences around a Gaussian patch is used instead. (Assuming zero-mean noise, the sum of differences around the same patch should be close to zero.) This threshold alone can cause noisy artifacts, so we simply enforce spatial smoothness using Markov random field defined on a standard 4-connected grid. The label set is $\{0, 1\}$ where 0 means the original pixels should be used and 1 means the computed average should be used. The energy functional decomposes into a dataterm $\phi$ and a smoothness term $\psi$:

We encode the color theshold into the dataterm as follows:

$\phi(x_i=0) = \beta_0 - \alpha\|D^i_{uv}\|^2$

$\phi(x_i=1) = \beta_1$

A hard threshold on $D^i_{uv}$ can be achieved by using some appropriate set of $\alpha, \beta_0, \beta_1$. The smoothness term is only non-zero when $\psi(x_i, x_j \neq x_i) = \gamma$ which penalizes different adjacent labels. This binary segmentation problem is solved using graph-cut which gives us a global-optimal labeling $X: \mathbb{R}^d \rightarrow \{0,1\}$. We then erode this labeling function and apply Gaussian blur to transform 0-1 labeling into a continuous alpha mask. The final low-noise composite is computed using a simple interpolation $(1-x_i)I^0 + x_i\widetilde{I^0}$.

Experiments

This section will go over some of the experiment results both that work and didn't work. In the first week, we tried a variational dense optical flow algorithm to accurately estimate the motion and perform a simple average. This gives us a baseline quality for denoising algorithms. The runtime however turns out to be impractical for real-time applications as the algorithm took 23 minutes to process 15 frames at resolution 960 x 540 pixels.

Left: cropped input. Right: cropped output using dense optical flow
In an attempt to make it faster, we tried different approaches and experimented with bilateral filtering on Permutohedral Lattice that spans across multiple frames in the video without doing any motion estimation. The amount of noise in uniform-color regions is reduced but when compared to a result using a high-quality dense optical flow, the image edges that are corrupted due to noise cannot be recovered or denoised properly.

Left: cropped input. Right: cropped output using bilateral filtering
Another method that we have explored is non-local means with Gaussian KD-tree, and we tried non-local means where feature vectors are pixels in an image patch. The computation was expensive and it has been shown by [Tasdizen] that dimensionality reduction in the feature vectors e.g. through PCA, produces superior results. We did not go beyond the described experiments as computing PCA also seems expensive in terms of time and memory and less promising than our current approach.

We discovered Farneback's algorithm based on polynomial expansion which runs very fast (less than a second) compared to a variational approach (100 seconds), but it cannot handle large motions and the flow seems to be inaccurate around the untextured regions.


Two frames that we test two optical flow algorithms on.
Left: color-coded flow field from Farneback's algorithm. Right: flow field from Ce Liu's implementation. Notice that the flow field from Farneback's algorithm isn't propagated correctly to untextured regions.

In order to handle larger motions with Farneback's algorithm, we therefore perform a global alignment using homography before running the dense optical flow as in our current pipeline. This hugely improves the alignment quality as shown below.


Left shows Farneback's warps without doing global alignment first. Right shows warps with global alignment which appears almost identical to the left image.

When we compare our results that use fast Farneback's optical flow to ones that use variational approach, the quality does not visually degrade on many datasets that we tried while running orders of magnitude faster.


Left shows a result from variational optical flow. Right shows a result with Farneback's optical flow + global alignment.
Another problem we had when we tried our algorithm on portrait photos was the ghosting artifacts. By adding similarity-based weights to the averaging process, the algorithm can handle some degree of scene motion and performs particularly well when there are enough frames similar to the reference.


Photos on the left are examples of ghosting artifacts and photos on the right are results using similarity-based averaging.

However, when the video clip contains large movements and there are no other frames that have similar scene appearance to the reference frame, the similarity-based weights can produce another kind of artifacts shown below.



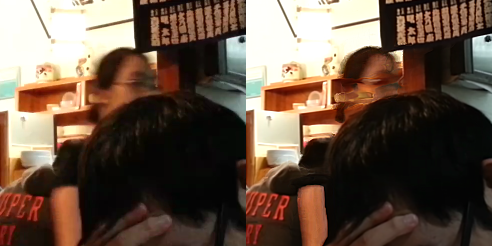
Top shows the input video sequence. Bottom left shows the reference frame and bottom right shows a result from similarity-based averaging.

We overcome this problem by applying threshold on color difference and retain the original pixel when the difference is too high. Together with smoothness term in MRF, we are able to handle pixels that appear a few times or once in the reference frame without producing the above artifacts or ghosting.


Comparing results without MRF on the left and with MRF and thresholding on the right.

Results

The algorithm handles still scenes with handheld captures very well and can handle large degree of scene/subjects' motions. The runtime of our algorithm on a single core for an image of size 960 x 540 is 8 seconds for 15 frames and 15 seconds for 30 frames. GIF animations on the left show video clips used to produce low-noise stills on the right. Each middle image is the reference (first) frame used in denoising.









Limitations

Our algorithm relies on SURF feature detector which can fail when there is no texture in the scene or the scene is very dark. Also, motions that appear in very dark regions tend to be ignored in the optical flow. Since the algorithm uses a uniform threshold, it does not compensate for the fact that human is more sensitive to dark pixel varations which can make the color in the result look different from the reference.


Bottom-left is the reference frame. Bottom-right shows our result. Note the color difference in the man's boot on the right.

Future work

To address the uniform-threshold problem, we can estimate the noise variance for different intensity levels, apply gamma correction, or perform computation in radiance space. Also, we plan to make the algorithm run on mobile phones or at least creating a video-clip capturing app which automatically captures 1-second clip with a shutter click.

References